Invarijantnost

Invarijantnost, općenito, je nepromjenljivost. U matematici i fizici invarijantnost je svojstvo pojedinih veličina, matematičkih objekata, funkcija, sustava i tako dalje da se ne mijenjaju pri nekim transformacijama ili pretvorbama (na primjer pri transformaciji koordinata).

Lorentzove transformacije: prostorno-vremenske koordinate događaja, koje mjeri svaki promatrač u svom inercijalnom referentnom okviru (u standardnoj konfiguraciji), prikazane su u govornim oblacima.
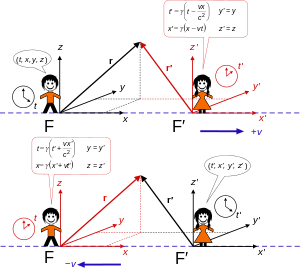
Gore: okvir F' se kreće brzinom v duž osi x okvira F.
Dolje: okvir F kreće se brzinom −v duž osi x okvira F' .

Lijevo: promatrač u mirovanju mjeri vrijeme 2L/c između lokalnih događaja stvaranja svjetlosnog signala u A i dolaska u A. Desno: događaji prema promatraču koji se kreće lijevo od postavke: donje ogledalo A kada se signal stvara u trenutku t '= 0, gornje ogledalo B kad se signal reflektira u vremenu t ' = D/c, donje ogledalo A kad signal vraća u vremenu t '= 2D/c.

Lorentzov faktor kao funkcija brzine (u prirodnim jedinicama gdje je c = 1). Napominjemo da je za male brzine (manje od 0,1) γ približno jednak 1.

Jedna od temeljnih simetrija u fizici je invarijantnost fizičkih zakona na Lorentzove transformacije: jednadžbe fizike trebaju imati isti oblik u svim inercijskim sustavima. U modernoj fizici elementarnih čestica, invarijantnost se općenito postiže zapisom veličina i jednadžbi u 4-vektorskoj formulaciji, po uzoru na 4 koordinate prostor–vremena u posebnoj teoriji relativnosti.

Invarijanta

Invarijanta, u fizici, je općenito svojstvo nepromjenljivosti ili simetrije u odnosu na neke promjene fizikalnih uvjeta, odnosno zahvate na fizikalnome sustavu. Invarijantnost prirodnih zakona uočena je najprije kao neovisnost o izboru prostorno-vremenskoga koordinatnoga sustava (x, y, z, t) u kojem se opisuje prirodna pojava. Invarijantnost (simetrija) na pomak ishodišta pretpostavlja da rezultat nekoga pokusa ne smije ovisiti o dijelu svemira u kojem se taj pokus izvodi. Slična se invarijantnost odnosi na prostorne rotacije (orijentaciju laboratorija prema udaljenim zvijezdama). Takvoj homogenosti i izotropnosti prostora dodaje se i zahtjev homogenosti vremena, to jest rezultat pokusa ne smije ovisiti o povijesnom trenutku u kojem se pokus izvodi. Te prostorno-vremenske simetrije imaju za posljedicu zakone očuvanja impulsa, impulsa vrtnje (zakretnoga momenta) i energije.

Korak je dalje zahtjev posebne teorije relativnosti da prirodni zakoni jednako glase u svim inercijskim sustavima. To povlači takozvanu kovarijantnost fizikalnih zakona, koju opća teorija relativnosti poopćuje i na neinercijske sustave. Očuvani naboji (primjerice električni naboj) vezani su uz takozvane globalne simetrije na transformaciju faza, dok lokalna (prostorno-vremenski ovisna) realizacija takvih simetrija, poznata pod nazivom baždarnih (engl. gauge) simetrija, ima vodeću ulogu u fizici elementarnih čestica pri formulaciji temeljnih međudjelovanja (interakcija).

Lorentzove transformacije

Lorentzove transformacije (po H. A. Lorentzu) su algebarske linearne relacije koje povezuju koordinate (x, y, z, t) nekoga fizičkog događaja u mirnome sustavu S (x, y, z, t) s pripadajućim koordinatama (x', y', z', t' ) u sustavu S' (x', y', z', t' ) koji se prema sustavu S giba uzduž osi x stalnom brzinom v. One se danas izvode, dokazuju i tumače iz dva postulata Einsteinove posebne teorije relativnosti (1905.):

1. postulata o konstantnosti brzine svjetlosti c u svim inercijskim sustavima bez obzira na brzinu sustava, izvora ili detektora svjetlosti, te
2. postulata kovarijantnosti da prirodni zakoni moraju imati isti oblik u svim inercijskim sustavima.

Polazeći od toga da svjetlosni signali (fotoni) putuju brzinom c u oba sustava i da se pravocrtna gibanja iz jednoga, kao takva, vide i u drugom sustavu i obratno (x = c∙t i x' = c∙t' ), kao i od načela relativnosti (zamjene uloge sustava S i S' i koordinata u njima), dobivaju se uz odgovarajući algebarski formalizam Lorentzove transformacije u obliku:

$t'=\gamma \cdot (t-{\frac {v}{c^{2}}}\cdot x)$

$x'=\gamma \cdot (x-v\cdot t)$

$y'=y$

$z'=z$

gdje se γ uobičajeno naziva Lorentzovim faktorom i vrijedi:

$\gamma ={\frac {1}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}={\frac {1}{\sqrt {1-\beta ^{2}}}}$

Obratne (inverzne) transformacije dobivaju se zamjenom v s –v u već napisanim odnosima, na primjer:

$t=\gamma \cdot (t'+{\frac {v}{c^{2}}}\cdot x')$

$x=\gamma \cdot (x'+v\cdot t')$

$y=y'$

$z=z'$