Indeks prelamanja
Indeks prelamanja
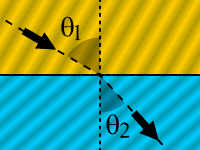
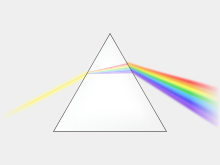
Indeks prelamanja zavisi od talasne dužine (frekvencije) svetlosti što se eksperimentalno ispoljava u pojavi spektra kada se zrak polihromatske (bele) svetlosti propusti kroz prizmu.
Indeks prelamanja je važna osobina materijala i zato se brižljivo meri (refraktometrom) i tabulira.
Definicije
urediIndeks prelamanja ima mnogo dublje značenje pogotovu što može da se poveže sa drugim osobinama materijala i saglasno tome može se definisati na više načina.
Striktno govoreći, indeks prelamanja je odnos koji pokazuje za koliko puta je fazna brzina elektromagnetnog (EM) zračenja u njemu, , manja u odnosu na brzinu u vakuumu, . Obično se obeležava simbolom , i za materijal definiše kao:
U materijalu sa ideksom prelamanja 1,5 = 3/2 brzina svetlosti iznosi tačno 2/3 brzine svetlosti u vakuumu, približno 200.000 km/s.
Pošto je brzina svetlosti (elektromagnetnih talasa) povezana sa eletričnim i magnetnim osobinama materijala indeks prelamanja se ekvivalentno može izraziti i relacijom:
gde je relativna (dielektrična) permitivnost materijala, a relativna (magnetna) permeabilnost. Za nemagnetne materijale je vrlo blisko jedinici pa je približno jednako . Fazna brzina predstavlja brzinu kojom se kreće vrh talasa, dakle, brzinu kojom se kreće faza talasa. Grupna brzina je brzina kojom putuje obvojnica talasa.
Brzina svetlosti
urediBrzina prostiranja elektromagnetnih talasa u vakuumu, c, je ista za sve vrste zračenja i približno iznosi 3×108 metara u sekundi. Dakle, ako je v fazna brzina zračenja određene frekvencije u datom materijalu, indeks prelamanja je dat izrazom:
Ovaj broj je tipično veći od jedan: što je veći indeks prelamanja svetlost se u materijalu sporije kreće. Međutim, na nekim frekvencijama (recimo u blizini apsorpcione rezonancije ili kod h-zraka) n postaje manje od jedinice. To ne protivureči teoriji relativnosti prema kojoj signal koji nosi informaciju ne može da se kreće brzinom većom od c, jer fazna brzina nije ista kao i grupna brzina kojom se informacija prenosi.
Ponekad se definiše i „indeks prelamanja grupne brzine“, grupni indeks:
gde je vg grupna brzina. Ovaj indeks ne treba mešati sa n koji se uvek odnosi na faznu brzinu.
Smanjenje fazne brzine može se objasniti i klasičnom slikom na mikroskopskoj skali. Promenljivo električno polje EM talasa navodi na dodatne oscilacije naelektrisanja u materijalu što se zbog njihove male mase, uglavnom odnosi na elektrone. Dakle, sveprisutni elektroni (iz atoma i molekula od kojih je sačinjen materijal) osciluju pod uticajem EM talasa ali zbog postojećih privlačnih sila između elektrona i atomskih jezgara, koje se suprotstavljaju poremećaju, oscilacije malko kasne u odnosu na oscilacije EM talasa. Svako naelektrisanje prilikom promene brzine emituje sopstveno zračenje, pa tako i elektroni koji osciluju pod uticajem EM talasa. To zračenje ima istu frekvenciju kao i pobudni EM talasi, ali malo kasni u fazi za EM talasima. Makroskopska suma svih elementarnih izvora je novi EM talas sa istom frekvencijom kao i pobudni ali sa nešto manjom talasnom dužinom. Dakle, do usporavanja faze dolazi zbog smanjenja talasne dužine EM zračenja prilikom prolaska kroz materiju, koje je pak izazvano otporom koji pružaju elektroni u materijalu prinudnim oscilacijama. Ukupan efekat je da se umesto prvobitnog EM talasa čija energija je utrošena na prinudne oscilacije elektrona, kroz materijal prostire talas iste frekvencije, ali nešto manje talasne dužine. Međutim, novi mikroskopski izvori zračenja mogu nešto energije da emituju i u drugim pravcima što se eksperimentalno ispoljava kao raspršenje svetlosti (videti rasejanje svetlosti.
Ako su za dva materijala, na datoj frekvenciji, indeksi prelamanja poznati, tada se pomoću Snelovog zakona može izračunati ugao pod kojim se prelama EM talas date frekvencije pri prelasku iz jedne sredine u drugu.
Nedavna istraživanja sa mikrotalasima su pokazala postojanje negativnog indeksa prelamanja što se može dogoditi ako su i ε i μ istovremeno negativni. Takva pojava nije očekivana u prirodi, ali se može postići u takozvanim metamaterijalima i pruža mogućnost konstrukcije savršenih sočiva i drugih egzotičnih pojava poput obrnutog Snelovog zakona.
Disperzija i apsorpcija
urediU realnim materijalima do polarizacije ne dolazi istog momenta kada se materijal izloži polju. Polarizcija malo kasni za primenjenim električnim poljem što dovodi do pojave dielektričnih gubitaka. Dielektrični gubici se izražavaju preko kompleksne permitivnosti koja još zavisi od frekvencije. Realni materijali nisu ni savršeni izolatori, dakle, pomalo provode jednosmernu struju. Uzimajući u obzir dieletrične gubitke i provodljivost, može se definisati kompleksni indeks prelamanja:
gde se n, kao i pre, odnosi na promenu fazne brzine dok κ, koeficijent ekstinkcije, pokazuje meru u kojoj dolazi do apsorpcionih gubitaka kada EM talas prolazi kroz materijal. Obe veličine, n i κ zavise od frekvencije (talasne dužine) EM zračenja.
Zbog frekventne zavisnosti neophodno je navesti vakuumsku talasnu dužinu EM talasa kojima je indeks prelamanja meren. Obično se merenja vrše na nekoliko dobro definisanih spektralnih linija. Na primer, nD je indeks prelamanja na Frauenhoferovoj "D" liniji, centru žutog natrijumovog dubleta talasne dužine 589,29 nm.
Zavisnost indeksa prelamanja od frekvencije (izuzev u vakuumu gde sve frekvencije imaju istu brzinu, c) poznata je kao disperzija i zahvaljujući njoj prizma razlaže belu svetlost u spektralne boje. Optička disperzija je i glavni izvor hromatske aberacije sočiva. U spektralnom području gde materijal ne apsorbuje zračenje realni deo indeksa prelamanja raste sa frekvencijom zračenja. U blizini apsorpcionih maksimuma, međutim, zavisnost indeksa prelamanja od talasne dužine poprima složen oblik i n može da opada sa porastom frekvencije.
Anizotropija
urediIndeks prelamanja izvesnih sredina može da zavisi od polarizacije i smera kretanja svetlosti kroz sredinu. Ta je pojava poznata kao dvojno prelamanje ili anizotropija i njome se bavi kristalna optika. U opštem slučaju, dielektrična konstanta je tenzor drugog ranga (matrica 3 h 3) koji ne može da se opiše jednostavno prelo indeksa prelamanja izuzev kada je polarizacija duž glavnih optičkih osa.
U magnetno-optičkim i optički aktivnim materijalima, glavne ose su kompleksne (odgovaraju eliptičkoj polarizaciji) a dielektrični tenzor je kompleksni-Ermitski (za sredine bez gubitaka); za takve materijale ne važi simetrija po inverzije vremena i oni se koriste recimo za pravljenje Faradejevih izolatora.
Nelinearnost
urediJako električno polje vrlo intenzivne svetlosti, recimo laserskog zraka, može da promeni indeks prelamanja sredine kroz koju prolazi (nelinearna optika). Porast indeksa sa kvadratom polja (linearna zavisnost indeksa sa intenzitetom) naziva se optički Kerov efekat i dovodi do pojava kao što su samofokusiranje i samo fazna modulacija. Linearna zavisnost indeksa od jačine polja (što je moguće samo u materijalima bez inverzione simetrije), naziva se Pokelsov efekat.