Lorenzov atraktor

Lorenzov atraktor je kaotično preslikavanje, istaknuto po svom leptirolikom obliku. Preslikavanje pokazuje kako stanje dinamičkog sustava (tri varijable trodimenzionalnog sustava) vremenski evolvira u složenom, neponavljajućem uzorku, često opisanom kao lijepim^{[nedostaje referenca]}.

Trajektorija Lorenzovih jednadžbi, renderirana kao metalna žica kako bi se naznačio smjer i trodimenzionalna struktura

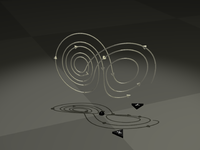
Sam atraktor, kao i jednadžbe iz kojih je izveden, je izmislio Edward Lorenz 1963., koji ih je izveo iz pojednostavljenih jednadžbi konvekcijskih uvrtanja koji izniču iz jednadžbi Zemljine atmosfere.^[1]

Sa tehničkog gledišta, sustav je nelinearan, trodimenzionalan i deterministički. 2001. je Warwick Tucker dokazao da za određene parametre sustav ispoljava kaotično ponašanje i pokazuje ono što je danas nazvano čudnim atraktorom. Čudni atraktor je u ovom slučaju fraktal Hausdorffove dimenzije između 2 i 3. Grassberger (1983.) je procjenio njegovu Hausdorffovu dimenziju na 2.06 ± 0.01 i korelacijsku dimenziju na 2.05 ± 0.01.

Sistem izniče u laserima, dinamima i specifičnim vodenicama [1].

Jednadžbe koje upravljaju Lorenzovim atraktorom su:

{\frac {dx}{dt}}=\sigma (y-x)

{\frac {dy}{dt}}=x(\rho -z)-y

{\frac {dz}{dt}}=xy-\beta z

gdje se $\sigma$ zove Prandtlovim brojem i $\rho$ Rayleighjevim brojem. Svi su $\sigma$ , $\rho$ , $\beta$ > 0, ali je obično $\sigma$ = 10, $\beta$ = 8/3 i $\rho$ varira. Sustav ispoljava kaotično ponašanje za $\rho$ = 28 i prikazuje čvoraste periodičke orbite za druge vrijednosti od $\rho$ . Primjerice, uz $\rho =99.96$ postaje T(3,2) torusni čvor.

Učinak leptira u Lorenzovom atraktoru

Učinak leptira

Vrijeme t=1 (povećano) Vrijeme t=2 (povećano) Vrijeme t=3 (povećano)

Ovi oblici - načinjeni uz ρ=28, σ = 10 i β = 8/3 - pokazuju tri vremenska segmenta 3-D evolucije dvaju trajektorija (jedne plavo, druge žuto obojeane) u Lorenzovom atraktoru počinjući od inicijalnih točaka koje se razlikuju svega za 10^-5 u x koordinati. U početku se dvije trajektorije podudaraju (vidi se samo žuta, jer je iscrtana preko plave) ali, nakon nekog vremena, očito divergiraju.

Java animacija Lorenzovog atraktora Arhivirano 2008-03-11 na Portuguese Web Archive-u pokazuje kontinuiranu evoluciju.

Rabeći različite vrijednosti za Rayleighjev broj

Lorenzov atraktor za različite vrijednosti ρ

ρ=14, σ=10, β=8/3 (povećano) ρ=13, σ=10, β=8/3 (povećano)

ρ=15, σ=10, β=8/3 (povećano) ρ=28, σ=10, β=8/3 (povećano)

Za male vrijednosti ρ, sustav je stabilan i evolvira u jednu od dvije fiksne točke atraktora. Kada je ρ veći od 24.74, fiksne točke postaju repulzori koji odbijaju trajektorije na vrlo složen način, evolvirajući bez presijecanja same sebe.

Java animacija koja prikazuje evoluciju za različite vrijednosti ρ Arhivirano 2008-03-11 na Portuguese Web Archive-u

Povezano

Izvori

Lorenz, E. N. (1963). „Deterministic nonperiodic flow”. J. Atmos. Sci. 20: 130-141. DOI:10.1175/1520-0469(1963)020%3C0130:DNF%3E2.0.CO;2.
Frøyland, J., Alfsen, K. H. (1984). „Lyapunov-exponent spectra for the Lorenz model”. Phys. Rev. A 29: 2928–2931.
Tucker, W. (2002). „A Rigorous ODE Solver and Smale's 14th Problem”. Found. Comp. Math. 2: 53-117.
Strogatz, Steven H. (1994). Nonlinear Systems and Chaos. Perseus publishing.
Jonas Bergman, Knots in the Lorentz system, Undergraduate thesis, Uppsala University 2004.
P. Grassberger and I. Procaccia (1983). „Measuring the strangeness of strange attractors”. Physica D 9: 189-208. DOI:10.1016/0167-2789(83)90298-1.

Eksterni linkovi

Lorenzov atraktor (MathWorld članak)
Lorenzova jednadžba Arhivirano 2009-06-07 na Wayback Machine-u na planetmath.org
Interaktivna animacija Lorenzovog atraktora (zahtijeva Adobe Shockwave dodatak)
Levitated.net: računska umjetnost i dizajn
3D VRML Lorenzov atraktor Arhivirano 2009-06-28 na Wayback Machine-u (zahtijeva dodatak VRML preglednika)
JAVA applet Arhivirano 2008-03-11 na Portuguese Web Archive-u - leptirov učinak, Lorenzov i Rosslerov atraktor
Eseji o Lorenzovim atraktorima u J-u - vidi programski jezik J

↑ [|ScienceDirect]. „Lorenz Equation”.

[1] [|ScienceDirect]. „Lorenz Equation”.

[1]

Učinak leptira
Vrijeme t=1 (povećano)	Vrijeme t=2 (povećano)	Vrijeme t=3 (povećano)

Ovi oblici - načinjeni uz ρ=28, σ = 10 i β = 8/3 - pokazuju tri vremenska segmenta 3-D evolucije dvaju trajektorija (jedne plavo, druge žuto obojeane) u Lorenzovom atraktoru počinjući od inicijalnih točaka koje se razlikuju svega za 10^-5 u x koordinati. U početku se dvije trajektorije podudaraju (vidi se samo žuta, jer je iscrtana preko plave) ali, nakon nekog vremena, očito divergiraju.
Java animacija Lorenzovog atraktora Arhivirano 2008-03-11 na Portuguese Web Archive-u pokazuje kontinuiranu evoluciju.

Lorenzov atraktor za različite vrijednosti ρ

ρ=14, σ=10, β=8/3 (povećano)	ρ=13, σ=10, β=8/3 (povećano)

ρ=15, σ=10, β=8/3 (povećano)	ρ=28, σ=10, β=8/3 (povećano)
Za male vrijednosti ρ, sustav je stabilan i evolvira u jednu od dvije fiksne točke atraktora. Kada je ρ veći od 24.74, fiksne točke postaju repulzori koji odbijaju trajektorije na vrlo složen način, evolvirajući bez presijecanja same sebe.
Java animacija koja prikazuje evoluciju za različite vrijednosti ρ Arhivirano 2008-03-11 na Portuguese Web Archive-u