Zlatni rez
Zlatni presek (simbol: ) je matematičko-strukturalni pojam kojeg se najčešće veže za umjetnost, jer je u istoriji umjetnosti najčešće korišten. To je način podjele neke vrijednosti s faktorom od približno 1.6.

1. Konstruiraj jedinični kvadrat (crveno).
2. Povuci liniju iz centra jedne stranice do suprotnog kuta.
3. Upotrijebi tu liniju kao radijus za iscrtavanje luka koji će odrediti dulju stranicu pravokutnika.

Zlatni presek je kompozicijski zakon u kojem se manji dio prema većem odnosi kao veći dio prema ukupnom. U praksi, ako želimo podijeliti nešto na taj način, podijelimo ga na 13 jednakih dijelova i onda to podijelimo u omjeru 8:5, ili ga pak podijelimo na 21 jednaki dio pa to onda u omjeru 13:8, itd. Na što se više dijelova podjeli, to smo bliži točnom zlatnom preseku, ali do tačnog zlatnog preseka nikada se ne dolazi jer je taj broj zapravo aproksimacija, a matematička formula glasi mu:
Teorija zlatnog preseka započeta je još u antici, a svoj procvat imala je u renesansi, kada su umjetnici i matematičari (ali i fizičari i astrolozi) tražili savršenstvo u kompozicijama poznatih struktura. Nakon mnogo stoljeća teorije smatra se da je zlatni presek najsavršeniji presek u prirodi, potpuno savršen ljudskom oku, harmonija između linearne, nepodnošljive preciznosti i nepravilne, netočne nesavršenosti.
U Italiji postoji mnogo primjera crkvi i dvoraca u toj kompoziciji. Također, na savršenom ljudskom tijelu sve je u odnosu 1:1.618.
Istorija
urediTeorija zlatnog reza započeta je u antici, a svoj procvat imala je u renesansi kada su umjetnici, matematičari, fizičari i astrolozi tražili savršenstvo u kompozicijama poznatih struktura.
Herodot (484. - 424. pne) „Jedan egipatski svećenik govoreći o obliku Keopsove piramide spomenuo mi je da je kvadrat nad njezinom visinom jednak površini bočnog trougla“
Grčki kipar Fidije u V vijeku pne.. primijenio je zlatni rez u dizajnu svojih skulptura i gradnji Partenona.
Platon (grčki filozof, V. i IV. vijek pne.) u „Timoteju“ opisuje pet pravilnih geometrijskih tijela kao osnovu harmonične strukture svijeta. Zlatni rez igra ključnu ulogu u dimenzijama i oblikovanju nekih od ovih tijela.
Pitagorejci (oko 500. god.pne.) dolaze do jednog od najvažnijih otkrića u matematici: - dijagonala i stranica kvadrata ( pravilnog peteugla) su nesamjerljive
Grčki matematičar Euklid prvi je ovaj broj uočio i matematički izrazio. Oko 300 godina prije Krista napisao je knjigu „Elementi“ u kojoj navodi prvu zabilježenu definiciju zlatnog reza.
Datu dužinu podijeliti tako da pravougaonik obuhvaćen cijelom dužinom i jednim odsječkom,bude jednak kvadratu na drugom odsječku.
Vijek pne sva znanja starih Grka objedinio je rimski arhitekt Marcus Vitruvius Polio u svom djelu „De architectura libri decem“ ili „Deset knjiga o arhitekturi“, posvećenom imperatoru Augustu. Pisao je o simetriji hramova, a njihove proporcije upoređuje s razmjerima čovječjeg tijela. Vitruvije je ucrtao ljudsko tijelo u kružnicu, što je kasnije ponovo interpretirao Leonardo Da Vinci
Fra Luca Pacioli (1446. - 1510.) štampao je u Veneciji 1509. djelo ”De divina proportione” koje je imalo veliki uticaj i nakon kojeg zlatni rez doživljava pravu renesansu. U njemu opisuje harmonijske osobine “božanske razmjere". Knjigu je ilustrirao Leonardo da Vinci.
Martin Ohm 1835. g. u drugom izdanju udžbenika Die reine Elementar -Mathematik ( Čista elementarna matematika ) prvi put koristi termin zlatni rez.
Oznaku je 1909. g. predložio američki matematičar Mark Barr u čast slavnom starogrčkom kiparu Fidiji (Phidias 480. -430.pne )
Izračunavanje
uredi| Spisak brojeva γ - ζ(3) - √2 - √3 - √5 - φ - α - e - π - δ | |
| Binarni | 1.1001111000110111011... |
| Decimalni | 1,6180339887498948482... |
| Heksadecimalni | 1.9E3779B97F4A7C15F39... |
| Neprekidni razlomak | |
| Algebarski oblik | |
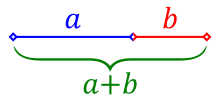
Za dvije veličine (pozitivni brojevi) a i b se kaže da su u zlatnom rezu ϕ ako vrijedi
Ova jednačina jednoznačno definiše ϕ.
Desna jednačina pokazuje da je a = bϕ, što se može zamijeniti u lijevi dio, dajući
Poništavanjem b na obe strane, dobijamo
Množenjem obe strane sa ϕ i premještanjem članova vodi do:
Jedino pozitivno rješenje ove kvadratne jednačine je
Prikazi broja
uredi


