Teseralna kristalna sistema
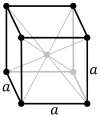
Kristalna rešetka teseralne sisteme okarakterisana je sa tri vektora elementarne translacije pa kristalografski osni krst ima tri ose (x,y,z) iste dužine i međusobno upravne.
a = b = c , α = β = γ = 90°
 |
 |
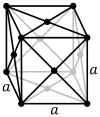 |
Kristalna rešetka je sa tri ose četvrtog stepena i moguće su tri Braveove rešetke: prosta, unutrašnje cenrirana i površinski centrirana.
Ukoliko se na kristalu javlja potpuni broj elemenata simetrije koji je karakterističan za taj vid kristalne rešetke tada taj kristal ima holoedrijski oblik. Ukoliko postoji redukcija u broju nekih elemenata reč je o parahemijedriji a ukoliko nedostaje centar simetrije reč je o antihemijedriji.
Teseralna holoedrija uredi
Prosti oblici u teseralnoj holoedriji su:
- Kocka ili heksaedar {001},
- Rombododekaedar {011},
- Ikositetraedar {hhl},
- Heksaoktaedar {hkl},
- Oktaedar {111},
- Tetraheksaedar {0kl},
- Trioktaedar {hll}.
Ove proste forme u procesu kristalizacije mogu se međusobno kombinovati i graditi različite kristalne kombinacije.
Pored holoedrije u teseralnoj sistemi kristali se javljaju i u parahemijedriji i antihemijedriji.
Teseralna parahemijedrija uredi
Prosti oblici teseralne parahemijedrije su:
- pentagondodekaedar {210} i
- dijakizdodekaedar {132}.
I u teseralnoj parahemijedriji u toku kristalizacije moguć je nastanak kristalnih kombinacija.
Kristali pirita FeS2 i Katijerita CoS2 mogu biti oblika pentagondodekaedra a pirit može imati kristale oblika dijakizdodekaedra.
Teseralna antihemijedrija uredi
Prosti oblici teseralne antihemijedrije su:
- tetraedar {111},
- trigondodekaedar {211},
- deltoiddodekaedar {221},
- hemiheksaoktaedar {132}.