Gaussov zakon magnetskoga polja
- Razlikovati od Gaussov zakon električnoga polja
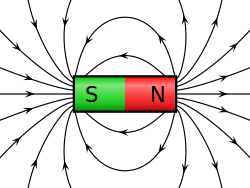
Gaussov zakon magnetskoga polja ili Gausov zakon magnetizma (po Carlu Friedrichu Gaussu) je fizički zakon po kojemu su silnice magnetskoga polja zatvorene linije, odnosno magnetski tok kroz zamišljenu zatvorenu plohu jednak je nuli (broj silnica koje ulaze u zatvorenu plohu jednak je broju silnica koje iz te plohe izlaze).[1] Tim je zakonom potvrđeno da u prirodi ne postoje magnetski monopoli.[1]
| Elektromagnetizam |

|
| Ključne stavke |
| Elektricitet • Magnetizam |
| Elektrostatika |
| Magnetostatika |
| Elektrodinamika |
| Električna mreža |
| Kovarijantna formulacija |
Naučnici
|
Gausov zakon magnetizma je uvršten među Maksvelove jednačine koje čine osnovu klasične elektrodinamike. Može biti izražen u dva oblika, u diferencijalnom obliku i integralnom obliku. Ove forme su prema teoremi divergencije jednake.
Zakon se takođe naziva i „Odsustvo slobodnih magnetskih polova“.[2]
Diferencijalni oblik uredi
Diferencijalni oblik Gausovog zakona magnetizama je:
Gde ∇• označava divergenciju, a B je magnetsko polje.
Integralni oblik uredi
Integralni oblik Gausovog zakona magnetizma iskazuje:
Gde je S bilo koja zatvorena površina (pogledati sliku desno), a dA je vektor, čija je veličina površina infitezimalnog dela površine S, i čiji je pravac okrenut ka spolja u smeru normale na površinu (videti površinski integral za više detalja). Leva strana ove jednačine se zove fluks magnetskog polja izvan površine, i Gausov zakon magnetizma navodi da je uvek nula. Integralni i difernecijalni oblici Gausovog zakona magnetizma su matematički ekvivalenti usled teoreme divergencije. Zato jedan ili drugi oblik mogu biti više pogodni za korišćenje u određenom proračunu.
Zakon u ovom obliku navodi da za svaki element zapremine u prostoru, postoji isti broj „linija magnetskih polja“ koje ulaze i izlaze iz zapremine. Nema ukupnog „magnetskog naelektrisanja“ koje se može nagomilati u nekoj tački u prostoru. Na primer, južni pol magneta je iste jačine kao i severni pol i slobodno plutajući južni polovi bez pratećih severnih polova (magnetski monopoli) nisu dozvoljeni. Kao suprotno, ovo nije tačno za druga polja kao što su električna ili gravitaciona polja gde ukupno električno naelektrisanje ili masa mogu da povećaju zapreminu prostora.
Prema vektorskom potencijalu uredi
Prema Helmholcovoj teoremi dekompozicije, Gausov zakon magnetizma je ekvivalentan sledećoj izjavi:[3][4]
Postoji vektor polja A tako da
- .
Vektor polja A se zove magnetski vektor potencijala.
Primetno je da postoji više od jednog mogućeg A koje zadovoljava ovu jednačinu za dato B polje. U stvari, ima ih beskonačno mnogo: svako polje oblika ∇φ može biti dodato na A da bi se dobio alternativni izbor za A po identičnosti (pogledati vektorski račun identičnosti):
Kako je iskrivljenje gradijenta nulto vektorsko polje:
Ova proizvoljnost u A se zove sloboda merila.
Prema linijama polja uredi
Magnetno polje B, kao bilo koje vektorsko polje, može biti prikazano putem linija polja (takođe zvanim fluks linijama)- to je, grupa krivih čiji pravci odgovaraju pravcu B i čija površinska gustina je proporcionalna intenzitetu B. Gausov zakon magnetizma je ekvivalentan izjavi da linije polja nemaju ni početak ni kraj: svaka, ili obrazuje zatvoreno kolo, uvija se zauvek bez vraćanja u pređašnje stanje ili se produžuje do beskonačnosti.
Modifikacije u slučaju da magnetski monopol postoji uredi
Ako bi magnetski monopol bio otkriven, onda bi Gausov zakon magnetizma navodio da bi divergencija B bila proporcionalna magnetskom naelektrisanju gustine ρm analogno Gausovom zakonu o električnom polju. Za nula gustinu magnetskog naelektrisanja mreže (ρm = 0), originalan oblik Gausovog zakona magnetizma je rezultat. Modifikovana formula u SI jedinicama nije standardna; u jednoj varijaciji, magnetsko naelektrisanje koristi jedinice vebera, a u drugoj koristi jedinice amper-metrima.
Jedinica Jednačina cgs jedinice[5] SI jednice (veber konvencija)[6] SI units (amper-metar konvencija)[7]
Gde je μ0 permeabilnost vakuuma.
Do sada nisu pronađeni magnetski monopoli uprkos detaljnom istraživanju.
Istorija uredi
Jednačina je bila jedna od Maksvelovih osam originalnih jednačina. Međutim, tumačenja su nešto drugačija: Maksvelovo A polje direktno odgovara važnom fizičkom kvantitetu koji je, kako je on verovao odgovarao Faradejevom elektrotoničnom stanju [8] dok moderno tumačenje naglašava slobodu merila, što je ideja da postoji mnogo mogućih A polja koja su sva jednako važna.
Literatura uredi
- Griffiths, David J.. Introduction to Electrodynamics , Prentice Hall. Šablon:Page1
- Jackson, John D.. Classical Electrodynamics , Wiley. Šablon:Page1
- Tipler, Paul. Physics for Scientists and Engineers: Electricity, Magnetism, Light, and Elementary Modern Physics , W. H. Freeman. Šablon:Page1
Izvori uredi
- ↑ 1,0 1,1 Gaussov zakon magnetskoga polja
- ↑ John David Jackson (1999). Classical Electrodynamics (3rd izd.). Wiley. str. 237. ISBN 978-0-471-30932-1.
- ↑ W.H.A. Schilders; E.J.W. Ter Maten (23. 5. 2005.). Handbook of Numerical Analysis. str. 13. ISBN 978-0-444-51375-5.
- ↑ John David Jackson (1999). Classical Electrodynamics (3rd izd.). Wiley. str. 180. ISBN 978-0-471-30932-1.
- ↑ F. Moulin (2001). „Magnetic monopoles and Lorentz force”. Il Nuovo Cimento B 116 (8): 869–877. arXiv:math-ph/0203043. Bibcode 2001NCimB.116..869M.
- ↑ John David Jackson (1999). Classical Electrodynamics (3rd izd.). Wiley. str. 273, eq. (6.150).
- ↑ See for example equation (4) in M. Nowakowski; N. G. Kelkar (2005). „Faraday's law in the presence of magnetic monopoles”. Europhysics Letters 71 (3): 346. arXiv:physics/0508099. Bibcode 2005EL.....71..346N. DOI:10.1209/epl/i2004-10545-2.
- ↑ Paul G. Hurray (2010). Maxwell's Equations. str. 22. ISBN 978-0-470-54276-7.